Let’s analyze this code and count how any operations it invokes. There is one assignment (count) before the for loop, plus another one inside (i). The for loop does $N + 1$ comparisons and $N$ updates (so $3 + 2N$ steps so far). On each iteration of the for loop (which executes $N$, we do one comparison and zero or one increments of count. So the total number of operations $R(N)$ is $3 + 3N \leq R(N) \leq 3 + 4N$. We can say that the execution time grows in the order of $N$, so the best way to describe the performance of the above snippet of code would be $\Theta(N)$. (It is also $O(N)$ and $\Omega(N)$.)

What is the order of growth $R(N)$, where $N$ is the size of numbers array?

The correct answer is A. $R(N) \in \Theta(1)$. Notice that the very first comparison is numbers[i] == numbers[j] where i and j are both zero. It is always the case that numbers[0] == numbers[0], so the function always returns true in constant time. Notice that even though there are two for loops, the order of growth is $\Theta(1)$ and not $\Theta(N^2)$.

Now, what is the order of growth $R(N)$, where $N$ is the size of numbers array?

The correct answer is D. Something else. It might seem that now that we’ve fixed the bug $R(N) \in \Theta(N^2)$. But that is only the case when we have to go through the entire array. For some arrays (e.g. an array of all zeros), we only have to compare the first two elements. So if the array contains just zeros, the function will execute in constant time regardless of the size of the array. Since the answer options have Big Theta and not Big O, the answer is something else (depends on the input). It is true, however, that $R(N) \in O(N^2)$.

What is $f \left( N \right)$?

Notice how the outer for loop starts executing with i = 1, so we print "hello" one time one the first iteration (the inner for loop starts with j = 0 and executes so long as j < 1). On the second iteration of the outer loop, i is 2 and the inner for loop executes two times. On the third iteration of the outer loop, i is 4 (since each time we multiply i by 2) and we print "hello" four times. So when n is 4 (or 5, 6 or 7) "hello" is printed 1 + 2 + 4 = 7 times.

Finally, consider this table that computes $R(N)$ for different values of $N$.

So we can see that $R \left( N \right)$ is always the next power of two minus one. Observe that for each $N$, $R \left( N \right) \leq 2N$. In fact, we can add a new column to the above table to demonstrate that.

From the above table we see that if $N$ is a power of two, $R \left( N \right)$ is $2N - 1$. For all other $N$, $R \left( N \right)$ is less than $2N - 1$. In general, $R \left( N \right)$ is the sum of all powers of two that are less than or equal to $N$. It turns out that this sum increases linearly, with a constant factor of 2. And so the correct answer is C. $N$.

Again, try to find a simple function $f(n)$ such that the runtime $R(N) \in \Theta \left( f \left( n \right) \right)$. What is $f \left( N \right)$?

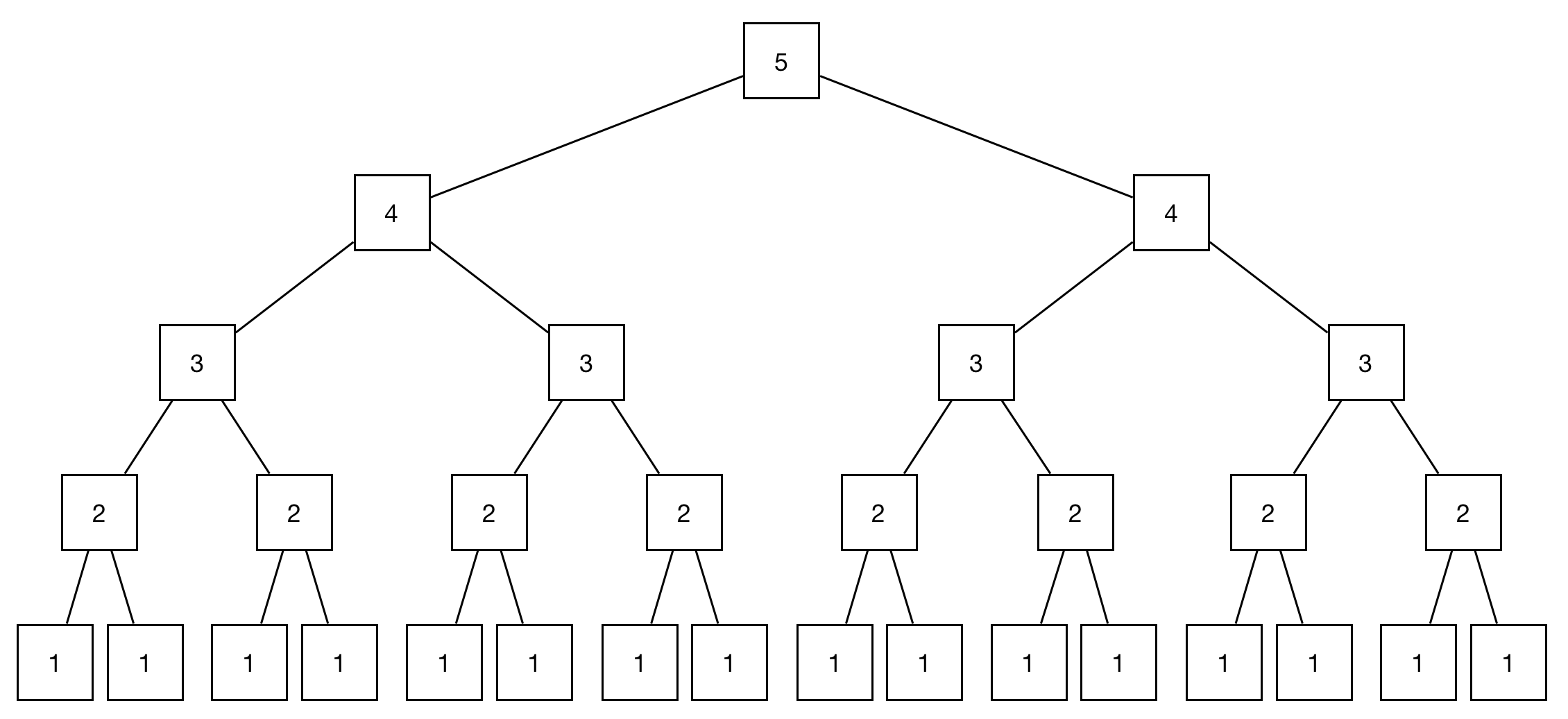
Notice that each node has two children. Also notice that the height of the tree is $N$.

We’ll come up with a recurrence relation that will express the number of steps the code has to execute and will help us find the overall complexity of the code. To do that, we’ll count the number of calls to recursive ($T(N)$) for an input of size $N$.

$T(N) = 2 T \left( N - 1 \right) + 1$

We can expand this recurrence relation a few times until we find a pattern.

$\begin{aligned} T(n) &= 2 T \left( N - 1 \right) + 1 \\ &= 2 \left( 2 T \left( N - 2 \right) + 1 \right) + 1 \\ &= 2 \left( 2 \left( 2 T \left( N - 3 \right) + 1 \right) + 1 \right) + 1 \\ &= 2 \left( 2 \left( \cdots 2 \cdot 1 + 1 \right) + 1 \right) + \cdots 1 \\ &= 2 \left( \left( \cdots 2 \right) \cdot 1 + 1 \right) + \cdots 1 \\ &= 2^{N - 1} + 2^{N - 2} + \cdots + 1 = 2^N - 1 = \Theta \left( 2^N \right) \\ \end{aligned}$

The intuition to solving this is that there are $N - 1$ 2s in the expanded version. (There are $N$ levels in the above binary tree and each node expcept the leaves has two children.)

To confirm, we can count the number of nodes on each level in the above tree.

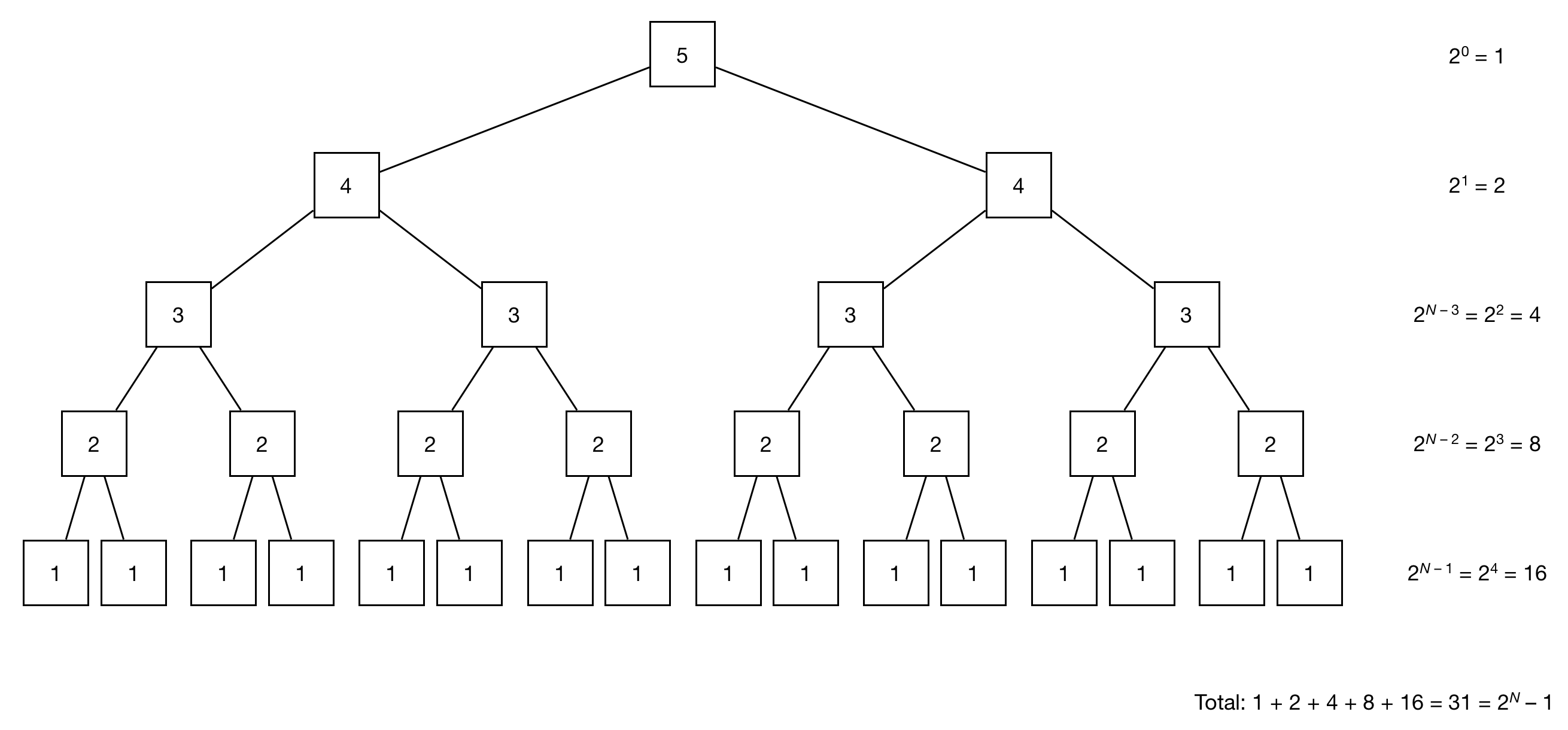
Therefore, the correct answer is F. $2^N$.