Sequence Containers

Array

STL’s array class is a very thin layer around C++ arrays. This container class manages its elements in an array of fixed size, so you must specify its size upon creation and cannot change the number of elements thereafter. As a result, size is part of the type.
```
array<int, 5> numbers = {1, 2, 3, 4, 5};
array<int, 4> moreNumbers = {10, 11, 12, 13};

// numbers and moreNumbers are of different type.
```
Creating an object of array class doesn’t give you much more power than what you’d get with regular static arrays, but it provides you with the ability to use STL’s functions such as begin, end, size, swap, etc.

Vector

A vector manages its elements in a resizable dynamic array. Therefore, it provides random access and you can retrieve elements in constant time. In addition, it has these properties:
- Adding new elements ad the end of the vector and removing elements from the end is very fast and takes $O(1)$ amortized time.
- Inserting and removing elements in the middle or in the beginning of the vector takes linear time, since the elements in the array used by the vector have to be moved over.
- Searching is also slow and takes $O(n)$ time.
There are two ways to access elements in a vector.
- Operator [] doesn’t perform a range check and may result in a segmentation fault (if you are lucky).
- std::vector::at method performs a range check and throws a out_of_range exception if its argument (of unsigned integral type) is greater than or equal to vector’s size.
Vector container class supports resizing, so that you need not know a priori how many elements you will ultimately store. So when you insert an element and the vector’s size has reached the capacity of the array used underneath the hood, vector will allocate a new dynamic array, will copy the old elements over and will insert the new element.

If the capacity were increased by 1 each time, then vector would have to resize on each insertion. That would be very costly, as that would involve allocating a new array on the heap and copying the existing elements over in addition to inserting the new element. So inserting $k$ elements would take $O(1 + 2 + \cdots + k) = O(k^2)$ time. Similarly increasing the array’s size by some constant other than 1 would be inefficient.

Doubling the size, on the other hand, turns out to be efficient. If we create a new array when the vector’s size reaches its capacity, we’d be doing work when we insert elements at indices 1, 2, 4, 8, 16, etc. Every time we create a new array on the heap, we copy the existing elements from the old array. So for $n$ elements we insert, we would be doing $O\left(1 + 2 + \cdots + \dfrac{n}{4} + \dfrac{n}{2} + n \right) = O\left( \left( 1 + \dfrac{1}{2} + \dfrac{1}{4} + \cdots + \dfrac{1}{n} \right) n \right) = O(n)$ work. If we divide this by $n$ , we’ll get $O(1)$ amortized time complexity for each insertion at the end. In amortized analysis, we take the total cost for a series of inputs and spread it across all inputs.
Since pushing elements to the end of the vector might make it resize by allocating a new array on the heap and deleting the old one, any iterators, pointers and references will be invalidated after insertion if new container size is greater than the previous capacity.

Deque

The term deque is an abbreviation for “double-ended queue”. It is a data structure implemented as a dynamic array that can grow in both directions. Similarly to the STL’s vector, it allows random access.

…

n0

n1

n2

n3

n4

n5

…
These are some of the properties of STL deques:
- Fast insertion and removal at the beginning and the end in constant time: $O(1)$ .
- Slow insertion and removal in the middle: $O(n)$ .
- Slow search in linear time: $O(n)$ .
A deque is implemented as non-contiguous chunks of dynamically-allocated memory and can be viewed in this way.^[1]
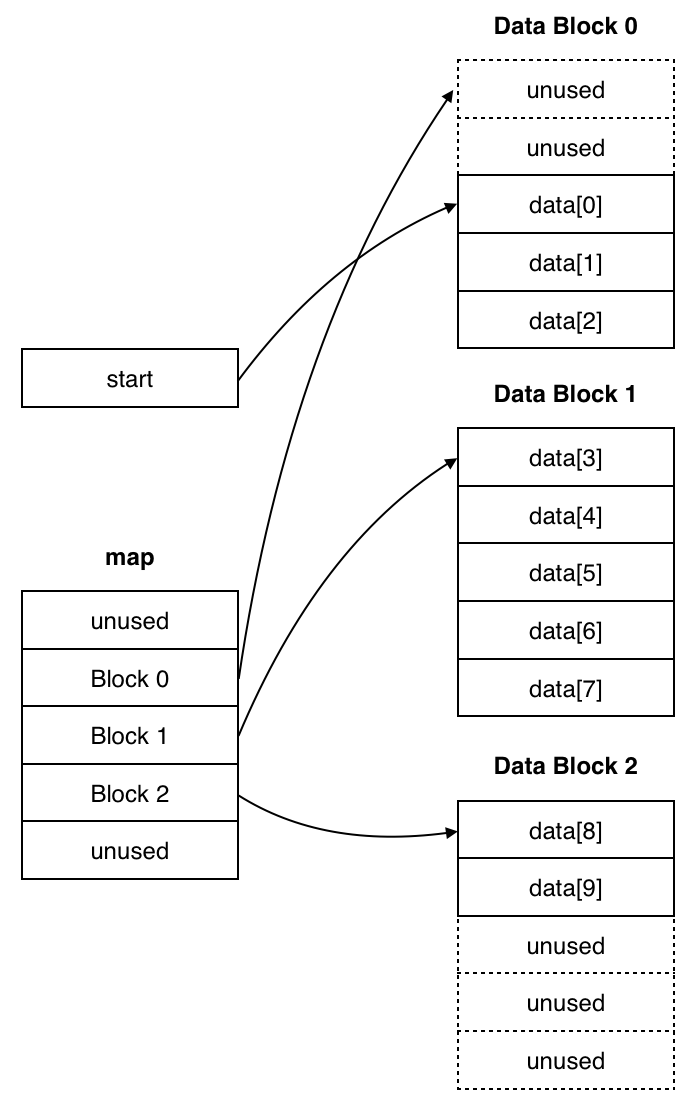
Similarly to vectors, iterators, pointers and references to objects in a deque may be invalidated after insertion.

List

The STL list is a doubly-linked list. Lists do not provide random access and do not support [] operator. As a result, lookup takes $O(n)$ time. However, insertion and removal at any position in a list are fast and take constant time. Search is still slow and takes $O(n)$ time.

Forward List

A forward list is just a restricted list that is implemented as a singly-linked list of elements.

1. Adapted from M. Nelson. 1995. C++ Programmer’s Guide to the Standard Template Library. IDG Books Worldwide, Inc.

Sequence Containers

Sequence Containers

Array

Vector

Deque

List

Forward List

results matching ""

No results matching ""