Graphs

  • A graph GG is a set VV of vertices and a set VV of edges that connect vertices. We can write this as G=(V,E)G = (V, E).

  • The difference between trees and graphs is that there can be more than one path between two nodes in a graph, and that a tree is connected and acyclic (cannot have a cylce).

  • There are two main types of graphs:

    • In directed graphs, every edge ee is directed from some vertex vv to some vertex ww.

    • In undirected graphs, edges connect vertices in no particular order.

  • Both directed and undirected graphs can have self-edges of the form (v,v)(v, v), which connect a vertex to itself.

  • A cycle is a path whose first and last vertices are the same.

    In an undirected graph, a path ⟨v0,v1,v2,...,vk⟩\langle v_0, v_1, v_2, ..., v_k \rangle forms a cycle if k≥3k \geq 3 and v0=vkv_0 = v_k.

    In a directed graph, a path ⟨v0,v1,v2,...,vk⟩\langle v_0, v_1, v_2, ..., v_k \rangle forms a cycle if v0=vkv_0 = v_k and the path contains at least one edge.

    The cycle is simple if, in addition, v0,v1,v2,...,vkv_0, v_1, v_2, ..., v_k are distinct. A self-loop is a cycle of length 11. A graph with a cycle is called cyclic. A graph without a cycle is called acyclic.

  • An undirected graph is connected if every vertex is reachable from all other vertices. A directed graph is strongly connected if every two vertices are reachable from each other.

  • Let’s now take a look at several examples of graphs.

    • Here is a graph representing Paris metro.[1] It is connected, undirected and cyclic.

      paris metro.png

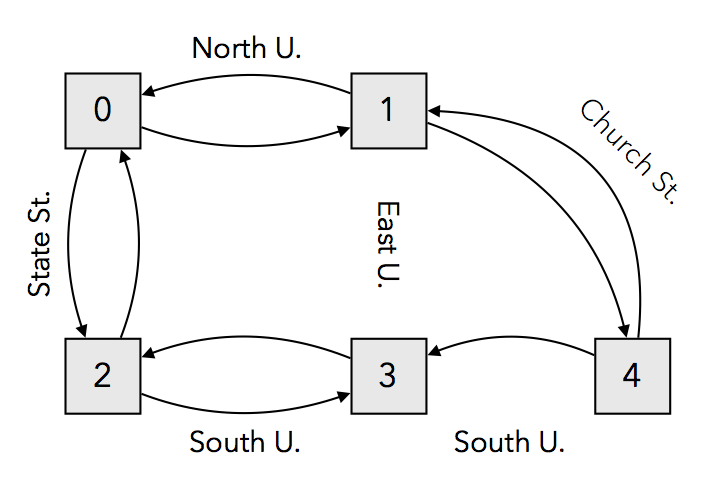
    • Here is a graph, where each node represents an intersection in Ann Arbor and each (labelled) edge represents a street. Notice while now on most streets, you can drive in both directions, you can only drive West on part of South U. (due to construction) and you cannot drive at all on East U. This graph is connected, directed and cyclic.

      a2.png

    • Finally, here’s a graph representing states (and one province!), where edges show the ability to cross borders between them. This graph is connected, undirected and cyclic.

      states.svg

  • A path is a sequence of vertices such that each adjacent pair of vertices is connected by an edge. If the graph is directed, the edges that form the path must all be aligned with the direction of the path.

  • The length of a path is the number of edges traversed by the path. Above, ⟨1,4,3,2⟩\langle 1, 4, 3, 2 \rangle is a path of length 33. A path can also be of length 00, such as ⟨3⟩\langle 3 \rangle.

  • The distance from one vertex to another is the length of the shortest path from one to the other.

  • The degree of a vertex is the number of edges incident on that vertex. In the graph above, Michigan has degree 4 and Ontario has degree 2. A vertex in a directed graph has an indegree (the number of edges directed toward it) and an outdegree (the number of edges directed away). Intersection 3 above has indegree 2 and outdegree 1.

  • Several kinds of graphs have special names.

    • A complete graph is an undirected graph in which every pair of vertices is adjacent.

    • A bipartite graph is an undirected graph G=(V,E)G = (V, E) in which VV can be partitioned into two sets V1V_1 and V2V_2 such that (v,w)∈E(v, w) \in E implies either v∈V1v \in V_1 and w∈V2w \in V_2 or v∈V2v \in V_2 and w∈V1w \in V_1. That is, all edges go between the two sets V1V_1 and V2V_2.

    • An acyclic, undirected graph is a forest.

    • A connected, acyclic, undirected graph is a free tree (not rooted tree).

    • We often call directed acyclic graph a dag.

Graph Representations

  • When we choose how to represent a graph G=(V,E)G = (V, E), it is important to consider the relationship between ∣V∣|V| (the number of vertices) and ∣E∣|E| (the number of edges).

  • The maximum possible number of edges is ∣V∣2|V|^2 for a directed graph, and slightly more than half of that for an undirected graph. However, the number of edges is often much less than Θ(∣V∣2)\Theta(|V|^2) in many applications.

    For instance, planar graphs (those that can be drawn without edges crossing, such as street maps) have at most ∣V∣|V| edges.

    In a complete graph, every vertex is connected to every other vertex.

  • A graph is sparse if ∣E∣|E| is much less than ∣V∣2|V|^2. A graph is dense if ∣E∣|E| is close to ∣V∣2|V|^2.

  • There are two standard ways to represent a graph G=(V,E)G = (V, E): as an adjacency matrix or as a collection of adjacency lists.

List of Edges

  • The simplest way to represent a graph is to just list all of its edges.

  • So for the graph of intersections above, we would list the edges as (0,1),(0,2),(1,0),(1,4),(2,0),(2,3),(3,2),(4,1),(4,3)(0,1), (0,2), (1,0), (1,4), (2,0), (2,3), (3,2), (4,1), (4,3).

Adjacency Matrix

  • In the adjacency-matrix representation of a graph G=(V,E)G = (V, E), we assume that the vertices are numbered 1,2,...,∣V∣1, 2, ..., |V| in some arbitrary manner. (∣V∣|V| is the number of vertices in the graph.) Then the adjacency-matrix representation of a graph G consists of a ∣V∣|V| by ∣V∣|V| matrix A=(aij)A = (a_{ij}) such that

    aij={1,if (i,j)∈E0,otherwise  a_{ij} = \begin{cases} 1, & \text{if } (i, j) \in E \\ 0, & \text{otherwise } \end{cases}

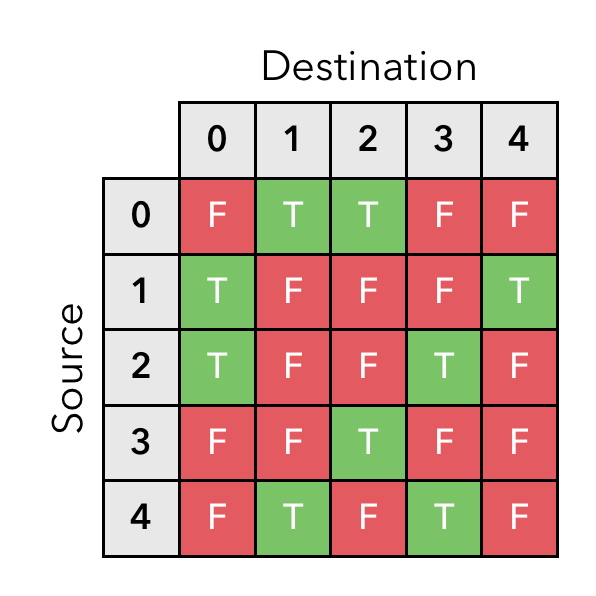
  • Here is how we could represent intersections of Ann Arbor shown above as an adjacency matrix:

    adjacency matrix.png

  • The total memory used for representing a graph as an adjacency list is Θ(∣V∣2)\Theta(|V|^2).

  • We prefer adjacency-matrix representation for dense graphs.

Adjacency List

  • The adjacency-list representation of a graph is an array of size ∣V∣|V|. Each element in the array is a list, one for each vertex in VV. For each vertex v∈Vv \in V, the adjacency list contains all the vertices (or pointers to the vertices) such that there is an edge (v,w)∈E(v, w) \in E. In other words, the the list contains all vertices adjacent to vv in GG.

  • Here is how we could represent intersections of Ann Arbor shown above as an adjacency list:

    adjacency list.svg

  • If vertices are not numbered 0,1,2,...,∣V∣−10, 1, 2, ..., |V| - 1 (e.g., if they are strings), we can use a hash table to map names to lists. Each entry in the hash table uses the object representing the vertex (e.g., its name) as a key, and a list as the associated value.

  • The total memory used for representing a graph as an adjacency list is Θ(∣V∣+∣E∣)\Theta(|V| + |E|).

  • We prefer adjacency-list representation for sparse graphs. And most real-world graphs are in fact sparse.

Weighted Graphs

A weighted graph is a graph in which each edge is labeled with a numerical weight. A weight might express the distance between two nodes, the cost of moving from one to the other or many other things.

  • In an adjacency matrix, weights is stored in the matrix. Whereas an unweighted graph uses an array of booleans, a weighted graph uses an array of numbers (int, double or another type). Edges missing from the graph can be represented by a sentinel value (such as 0, -1 or INT_MIN). Alternatively, we might use an array of booleans and an array of numbers to allow all numerical values to be valid weghts.

  • In an adjacency list, recall that each edge is represented by an array or a linked list of adjacent vertices. We could augment the nodes of the linked list that represents each edge to include a weight, in addition to the reference to the destination vertex. (Or if we are using arrays instead of linked lists, we could use two separate arrays: one for weights and one for destinations.)

  • There are two common problems involving weighted graphs:

    • The shortest path problem: find a path between two vertices in a graph such that the sum of the weights of of the edges along the path is minimized.

    • The minimum spanning tree (MST) problem: find which edges in the graph must remain such that the graph is connected, but the total weight in the remaining edges is minimized.

Graph Algorithms

results matching ""

    No results matching ""