AVL Trees

Recall that balanced BSTs maintain $h = O(\log n)$ , so all operations run in $O(\log n)$ time.
Self-balancing BSTs are data types that automatically keep track of their height to maintain the balanced property.
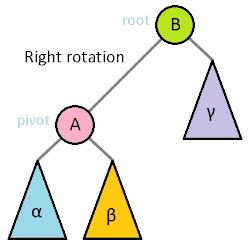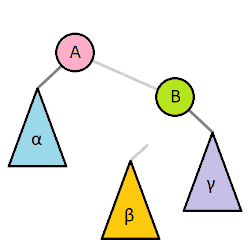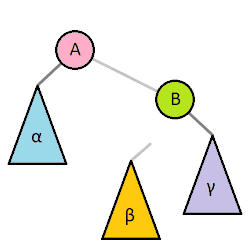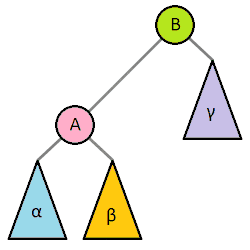
One of the most important operations on most self-balancing binary trees is the rotation. Left and right rotations are animated below.^[1]
Some of the popular data structures that implement self-balancing BSTs include:
- 2-3 trees
- AVL trees
- Red-black trees
In this section, we’ll discuss AVL trees.

AVL: Adel’son-Vel’skii & Landis

AVL trees are the first example (invented in 1962) of a self-balancing binary search tree.
AVL trees satisfy the height-balance property: for any node $n$ , the heights of $n$ ’s left and right subtrees can differ by at most 1.
To make math easier, we can define each null node to have height of -1. This will make balancing easier.
As part of data structure augmentation, each node stores its height. Alternatively, you can store just difference in heights.
We will call a node unbalanced if its left and right children differ in height by more than 1.

The find operation for an AVL tree exactly the same as for a binary search tree.
Since an AVL tree is guaranteed to be balanced, find always takes $\Theta(\log n)$ time in the worst case, where $n$ is the number of elements in the AVL tree.

To insert into an AVL tree,
1. Insert as into a simple BST.
2. Work your way up the tree, restoring the AVL property and updating heights as you go.
Take a look at the slides for an example of inserting a sequence of numbers.

For an AVL tree with $N$ nodes, searching, insertion and deletion each take $O(\log N)$ time.
The path from the root to the deepest leaf in an AVL tree is at most $\sim1.44 \log(N + 2)$ .

As you can see, AVL trees are difficult to implement.
In addition, AVL trees have high constant factors for some operations. For example, restructuring is an expensive operation, and an AVL tree may have to re-balance itself $\log_2 n$ in the worst case during a removal of a node.
Most STL implementations of the ordered associative containers (sets, multisets, maps and multimaps) use red-black trees instead of AVL trees. Unlike AVL trees, red-black trees require only one restructuring for a removal or an insertion.