Let’s consider several ways of generating hash codes for strings.

For example, we might want to map airport codes (such as DTW) to airport names like so.

int airportHash(const string &airportCode) {
    if (airportCode.length() != 3) {
        return -1;
    }
    return toupper(airportCode[0]) - 'A';
}

Let’s improve the hash function for airport codes such that each code in the universe of all possible three-letter codes has a unique integer hash code.

int airportHash(const string &airportCode) {
    if (airportCode.length() != 3) {
        return -1;
    }
    return 26 * 26 * (toupper(airportCode[0]) - 'A') +
                26 * (toupper(airportCode[1]) - 'A') +
                     (toupper(airportCode[2]) - 'A');
}

In general, a good way to generate hash codes for string

int string hash(const string &s) {
    int result = 0;
    for (int i = 0; i < s.length(); i += 1) {
        result = (result << 5) - result + s[i];
    }
    return result;
}

C++ Standard Library happens to have a functor that computes hash codes: std::hash<>. Standard specializations exist for all built-in types, and some other standard library types such as std::string and std::thread, and you can provide specializations for your own custom types if you’d like. The unordered associative containers (unordered set, unordered multiset, unordered map and unordered multimap) use specializations of the template std::hash as the default hash function.

A hash function’s output (often referred to as just hash), usually a 32-bit integer, is too large for the purpose of a practical application. If used as an array’s index, it would dictate the need for an array of size $2^{32}$ (~4 billion). And since each array element would at the very least be 4 bytes long (in the case of integers or 32-bit pointers), we would need 4 × 4 billion bytes ≈ 16 GB of memory.

And so we need to compress the hash code to reduce it to the size of the array we are using for the hash table.

The most common compression function is $c = h \bmod m$, where $c$ is the compressed hash code that we can use as the index in the array, $h$ is the original hash code and $m$ is the size of the array (aka the number of “buckets” or “slots”).

A problem with this hash function is that patters in keys (e.g., 4, 8, 12, 16) will cause collisions and clusters in the hash table, especially if $m$ (number of buckets) is a multiple of of 4. For example, suppose $m$ is $100$ or $200$. Three quarters of the buckets will never be used.

Here’s a better compressing function:

Since we use the hash function to determine where in the hash table to store a key and where in the hash table to search for the key, it is crucial for a hash function to behave consistently and output the same index for identical inputs.

Here are some properties of good hash functions to keep in mind:

Unfortunately, hash codes and compression functions are a somewhat a black art. The ideal hash code and compression function would map each key to a uniformly distributed independently chosen (“random”, in a sense) bucket between $0$ and $m - 1$. So the probability of two keys colliding would be $\dfrac {1}{m}$.

As you saw in the previous examples, it is easy to create hash functions that create more collisions than necessary.

Remember that collisions can happen at two steps:

In open addressing (or probing), we store the key-value pairs directly in the array. If a slot is occupied, we find another slot in the array using the hash function.

The hash function now takes two arguments: $k$, the key that we are inserting and $i$, the probe number. The hash function thus becomes

With open addressing, we require that for every key $k$, the probe sequence

Another constraint on open addressing is that the hash table can no longer hold more elements than there are buckets, so $n \leq m$ is always true.

To insert a new element, we hash its key to get the index of the slot in the array where we should insert, and then check if that slot is available. If it’s empty, we insert the new element, otherwise we call the hash function again to get a new index. We stop when we find an available slot or when we have checked all the slots in the hash table.

insert(key, value):
    i = 0
    while i ≠ m:
        index = hashFn(key, i)
        if array[index] == null:
            array[index] = (key, value)
            return index
        else:
            i = i + 1
    error "hash table overflow"

To find an element, we hash its key to get the index of the slot in the array. If the element exists and its key is the same, we insert the value (or the key-value pair), otherwise we call the hash function again to get a new index. We stop when we find a slot that is empty or when we have checked all the slots in the hash table.

find(key, value):
    i = 0
    do:
        index = hashFn(key, i)
        if array[index].key == key:
            return array[index].value
        else:
            i = i + 1
    while array[index] ≠ null or i ≠ m:
    error "hash table overflow"

Removing an element is more difficult. When we delete a key from slot i, we cannot simply mark it as null, since that would make the find operation stop early and fail to check the elements past this slot. We can solve this problem by marking the slot deleted (sometimes referred to as “ghost”) instead of null:

remove(key, value):
    i = 0
    while i ≠ m:
        index = hashFn(key, i)
        if array[index].key == key:
            array[index] = deleted
            return
        else:
            i = i + 1

insert(key, value):
    i = 0
    while i ≠ m:
        index = hashFn(key, i)
        if array[index] == null or deleted:
            array[index] = (key, value)
            return index
        else:
            i = i + 1
    error "hash table overflow"

We will now look at three commonly used techniques to compute the probe sequences required for open addressing: linear probing, quadratic probing, and double hashing.

In the separate chaining model, the hash table is actually an array of pointers to linked lists. When a collision occurs, the key can be inserted in constant time at the head of the appropriate linked list.

If we insert DTW, SFO, LHR, YYZ, LAX and SYD into a hash table and use separate chaining as the collision resolution schema, we’ll this hash table.

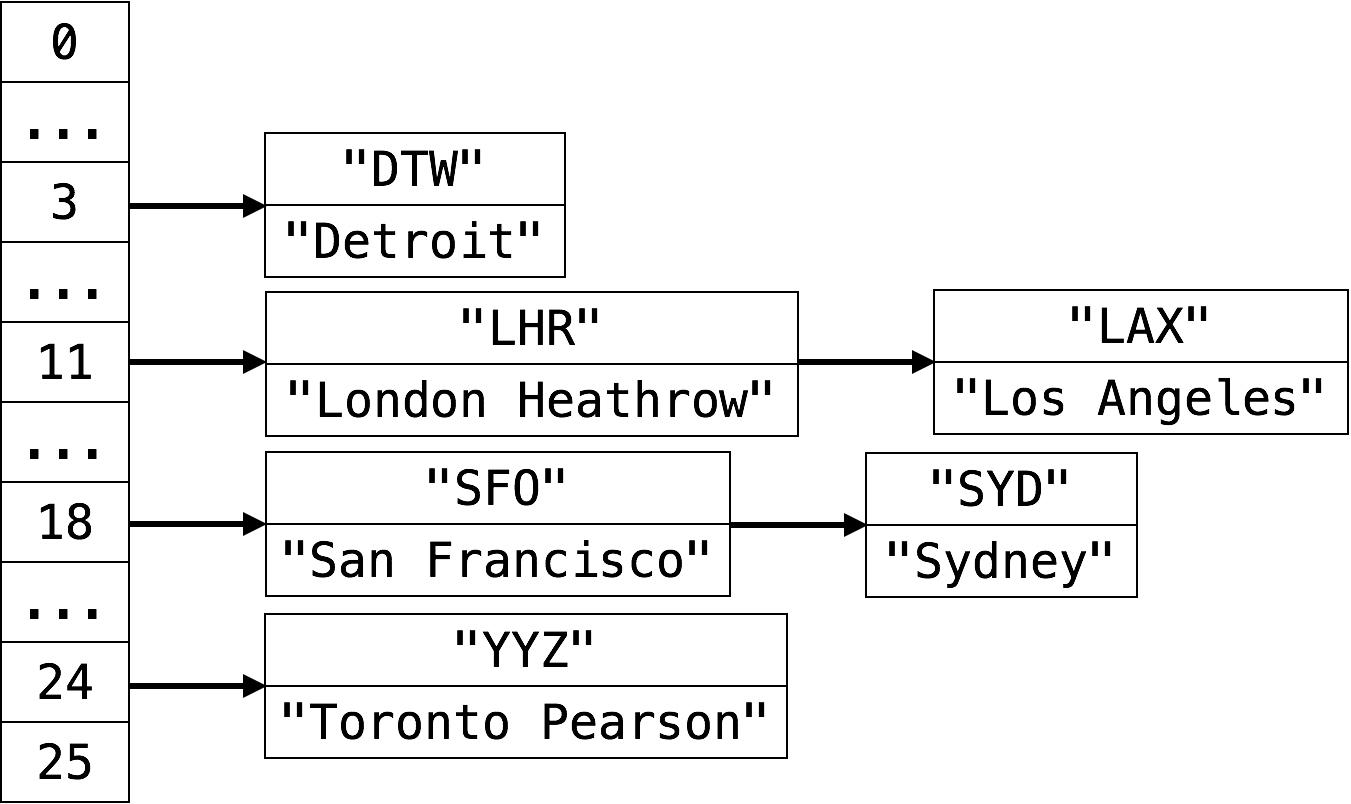
What happens now when we search for something like LAX in the hash table? We must traverse the entire linked list at index 11. The worst case lookup time for a hash table that uses separate chaining (assuming a uniform hash function) is therefore $O\left(\dfrac{n}{m}\right)$, where $m$ is the size of the hash table.

We define load factor $\alpha = \dfrac{n}{m}$, where $n$ is the number of items in the hash table and $m$ is the size of the array.

Since $m$ is a constant, $O\left(\dfrac{n}{m}\right)$ is theoretically equivalent to $O(n)$. In the real world, however, $O\left(\dfrac{n}{m}\right)$ is a big improvement over $O(n)$! A good hash function will maximize this real world improvement.