
Disjoint Sets
A disjoint set is a data structure that keeps track of a universe of elements. The items are partitioned into a number of disjoint (non-overlapping) sets, so no item can be in more than one set.
Operations
-
Disjoint sets support two useful operations:
-
Find: determine which set a particular element is in.
Find typically returns an item from this set that serves as its “representative”.
By comparing the result of two find operations, one can determine whether two elements are in the same subset.
-
Union: join two subsets into a single subset.
-
-
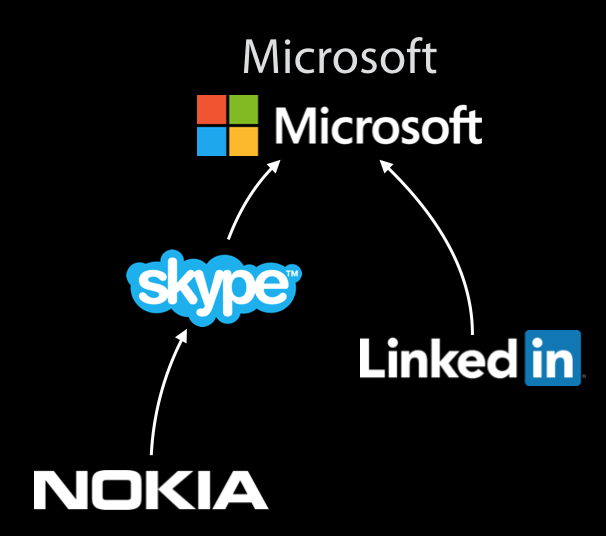
For example, suppose that in our universe we have seven items: Microsoft, Verizon, Nokia, Yahoo!, Tubmlr, Skype and LinkedIn.
-
Initially, each item is in its own set. Let’s represent each set with the item’s name.

If we perform the
findoperation on each item, we will get the set that contains that item:find(Skype) → Skype find(Tumblr) → Tumblr find(LinkedIn) → LinkedIn -
Now suppose Microsoft acquires Skype (we perform the
unionoperation on the sets that contain Microsoft and Skype). We choose to refer to the resulting set as Microsoft. In addition, Yahoo! acquires Tumblr (we perform theunionoperation on the sets that contain Yahoo! and Tumblr). We choose to refer to the resulting set as Yahoo!.
If we perform the
findoperation on each item, we will get the set that contains that item:find(Skype) → Microsoft find(Tumblr) → Yahoo! find(LinkedIn) → LinkedIn -
Let’s now suppose that we perform the
unionoperation on the sets Microsoft and Nokia, then on the sets Microsoft and LinkedIn, and then on the sets Yahoo! and Verizon. We might end up with these sets:
If we perform the
findoperation on each item, we will get the set that contains that item:find(Tumblr) → Verizon find(Yahoo!) → Verizon find(Verizon) → Verizon
-
-
We will distinguish two main implementation of disjoint sets: Quick Find and Quick Union.
Quick Find
-
Quick Find algorithm is a list-based representation of disjoint sets that supports a quick
findoperation. -
Each set references the list of items in that set.
-
Each item references the set that contains it.
-
findoperation takes time, since we only need to dereference the pointer that points to the set. -
unionoperation, however, is slow. When we join two sets, we need to go through each item in one of the sets and change the pointer that points to the set.
Quick Union
-
Quick Union algorithm is a tree-based representation of disjoint sets that supports a quick
unionoperation. -
Each set is stored as a tree and the entire data structure is a forest.
-
The root of the tree represents the true identity of the set.
-
Each item is initially root of its own tree.
-
Each item only has a parent pointer and has no child or sibling pointers.
-
To perform the
unionoperation, we make the root of one set be the child of the root of another set. Time complexity of theunionoperation is . -
To perform the
findoperation, we follow the parent pointer to the root. Time complexity of thefindoperation is proportional to the depth of the node.
Union by Size Optimization
-
To omptimize the complexity of the
findoperation, we want to prevent the items from getting too deep in the tree. -
At each root, we record the size of the tree. (Even though the size is not always equivalent to depth, we’ll use size as an approximation.)
-
For the
unionoperation, we make the smaller tree be a subtree of the larger one.
Array Representation
-
To represent the tree as an array, we make as assumption that the items in the universe are integers from to .
-
We use an array of size and each item is represented by the element in the array at index . If an item has a parent, we record the parent of that item in the array. Otherwise, the item is a root and we record the size of the tree as a negative number.
-
With an array representation, the code for the
unionoperation becomes as simple asvoid union(int root1, int root2) { if (array[root2] < array[root1]) { // root2 has a larger tree array[root2] += array[root1]; array[root1] = root2; } else { // root1 has a larger tree array[root1] += array[root2]; array[root2] = root1; } }
Path Compression Optimization
-
We observe that when we perform the
findoperation on an item, we traverse the tree by following the parent pointers up to the root. -
To optimize future
findoperation, we will change the parent pointer to the root of tree for each item on which we perform thefindoperation. -
The code for the
findoperation is now justvoid find(int x) { if (array[x] < 0) { // x is root return x; } else { array[x] = find(array[x]); return array[x]; } }
Complexity of Quick Union
-
The
unionoperation takes time. -
The
findoperation takes time in the worst case, where is the number of union operation. Average running time is close to constant. -
A sequence of
findoperations andunionoperations takes time in the worst case. is the inverse Ackermann function that is extremely slow-growing.