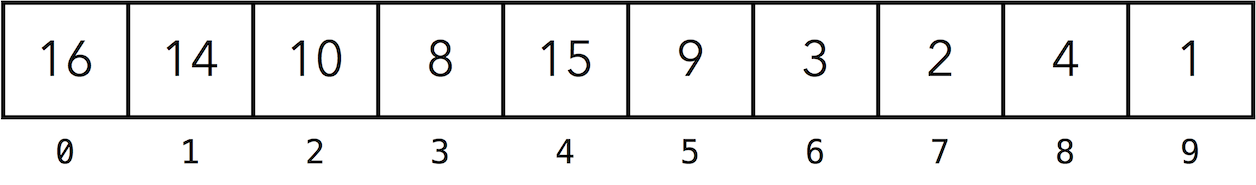
Heaps

The (binary) heap data structure is an array that represents a nearly complete binary tree.

Note	The heap data structure is completely unrelated to the region of the computer’s memory of the same name.

Note

A binary tree is a tree where every node has at most two children.

A complete binary tree is one where each node has 0 or two children and the total number of elements of a tree of height $h$ is $2^{h + 1} - 1$ . Notice how every level is completely filled and all leaves are at the same level.

A nearly complete binary tree is one where every level, except possibly the last, is completely filled. On the last level $h$ , it must have between $1$ and $2^h$ nodes.

Array Representation

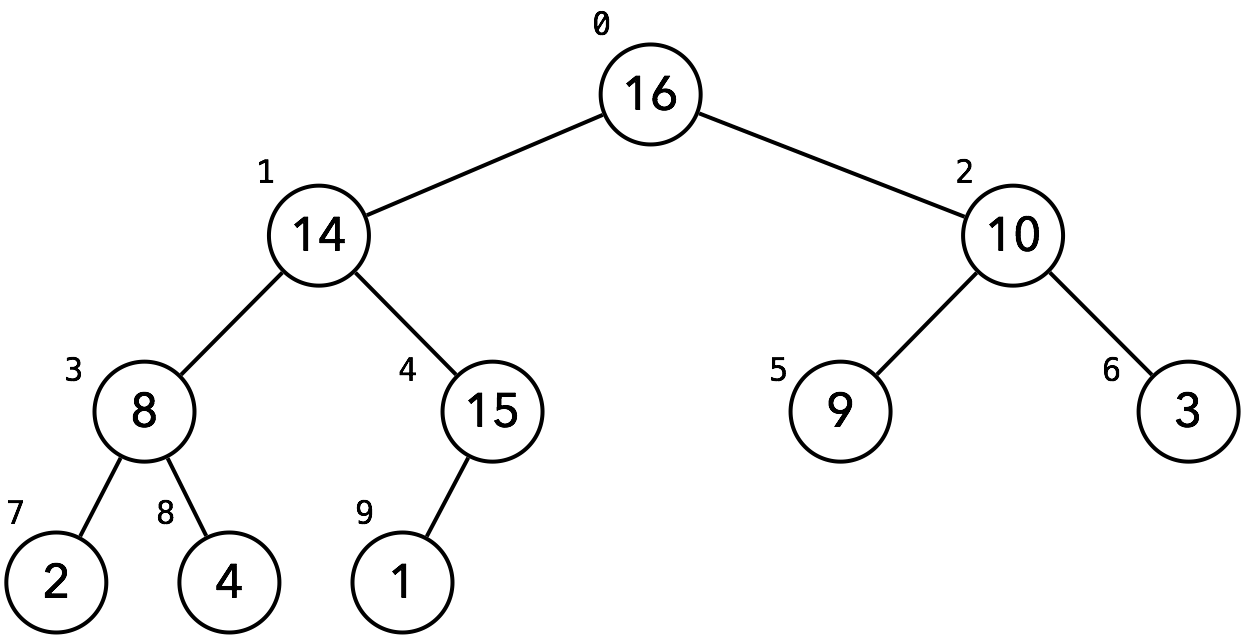
A binary heap is often represented as an array.
Below are the properties of such representation.
- The size of the array $n$ is the number of elements in the heap.
- The root of the tree is the first element in the array.
- The parent of the element at index $i$ is at index $\dfrac {i - 1}{2}$ .
- The left child of the element at index $i$ is at index $2i + 1$ .
- The right child of the element at index $i$ is at index $2i + 2$ .
- The height of the tree with $n$ elements is $\lceil \log (n + 1) \rceil$ .

Heap Property

There are two kinds of binary heaps: max-heaps and min-heaps. In both kinds, the values in the nodes must satisfy a heap property. For the remainder of this section, we will discuss max-heaps. Min-heaps are analogous.
In a max-heap, nodes must satisfy the max-heap property: every node must be greater than or equal to its children.
Below are some examples of valid max-heaps: all are nearly complete binary trees where the values in the nodes satisfy the max-heap property.

Heap Operations

maxHeapify

maxHeapify(i) corrects a single violation of the heap property in a subtree with root at i. This procedure assumes the left and right children of the element at i are valid max-heaps.
To correct a violation at index i, we find largest, the largest of left(i) and right(i). Then we swap the elements at indices i and largest (A[i] and A[largest]) and call maxHeapify(largest) until the violation no longer exists.
Here is an example of correcting a violation at index 1 by calling maxHeapify(8).

Pseudocode for maxHeapify, where A is the array representing the heap:

maxHeapify(i):
    l = left(i)
    r = right(i)
    if l < A.size and A[l] > A[i]:
        largest = l
    else:
        largest = i
    if r < A.size and A[r] > A[largest]:
        largest = r
    if largest ≠ i
        swap A[i] and A[largest]
        maxHeapify(largest)

Time complexity of maxHeapify is $O(\log n)$ where $n$ is the number of elements in the heap.

A more precise time complexity of calling maxHeapify(i) is $O(h)$ where $h$ is the height of the subtree with root at node i. If the number of elements in the subtree is $n_i$ , the time complexity is $O(\log n_i)$ .

buildMaxHeap

buildMaxHeap() produces a max-heap from an unordered array.
We observe that the leaves of the heap are always valid max-heaps. So to build a max-heap, we need to correct violations on nodes that are not leaves. (If the array that we use to represent our heap is 0-indexed, these would nodes at indices between $\dfrac{n - 2}{2}$ and $0$ inclusive).
Here is an example of building a max heap from an array containing the elements {4, 1, 3, 2, 16, 9, 10, 14, 8, 7.

Pseudocode for buildMaxHeap, where A is the array representing the heap:

buildMaxHeap():
    for i = (A.size - 2) / 2..≥0:
        maxHeapify(i)

A simple analysis of time complexity of buildMaxHeap on a heap with $n$ elements will lead to a complexity of $O(n \log n)$ , since we make $\dfrac{n}{2}$ calls to maxHeapify and each call takes $O(\log n)$ time.

However, we can get a tighter bound by doing a more careful analysis. Observe that each call to maxHeapify requires $O(h)$ time where $h$ is the height of the subtree at node $i$ . The number of nodes at height $h$ is $\dfrac{n}{2^h + 1}$ . Therefore, the running time is

$\begin{aligned} \sum ^{\log n}_{n = 0} \left( O(n) \times \dfrac{n}{2^n + 1} \right) &= O\left( n \sum ^{\log n}_{h=0} \dfrac{h}{2^h} \right) \\ &= O\left( n \sum ^{\infty}_{h=0} \dfrac{h}{2^h} \right) \\ &= O(n) \end{aligned}$

Since $\sum \limits_{h=0}^{\infty} \dfrac{h}{2^h} = 2$ .

Heaps

Heaps

Array Representation

Heap Property

Heap Operations

maxHeapify

buildMaxHeap

results matching ""

No results matching ""